Industrial simulation goes hand-in-hand with queuing systems. This is a very broad topic; we could spend hours talking about both theoretical aspects and practical applications with simulation software. Here, we will only compare two common types of lines.
Traditionally in France, in a queuing situation, customers choose a line in front of a counter and stay there until they are served. The initial choice is obviously oriented towards the shortest line. Though it is statistically reasonable, it does not guarantee that the customer will be served as quickly as possible, because the processing time can vary from one customer to another. You have certainly already experienced this frustrating situation in a supermarket, when the person before you presents an item with an illegible price and therefore entails a series of time-consuming operations, whereas customers at the other checkouts keep moving quietly though they arrived after you! 1)
There is another system which is widely spread in Anglo-Saxons countries and increasingly developed in France and which consists in a single line for all counters. Customers are served according to the first come, first served method. This system appears to be “fairer”.
One of our customers who works in the fast-food industry consulted us about this issue; we decided to compare these two systems strictly in terms of waiting time for customers.
Building the corresponding model was relatively easy. We took into consideration 5 identical counters. The processing time per customer is randomly decided following a uniform distribution between 10 and 50 seconds. In a simulation run set for 3 hours, customers appear randomly with an interval between arrivals that follows an exponential distribution (the Poisson representation) of 7 seconds on average. In separate lines customers choose the shortest line but cannot change lines at a later stage.
Here is the model built with ExtendSim:
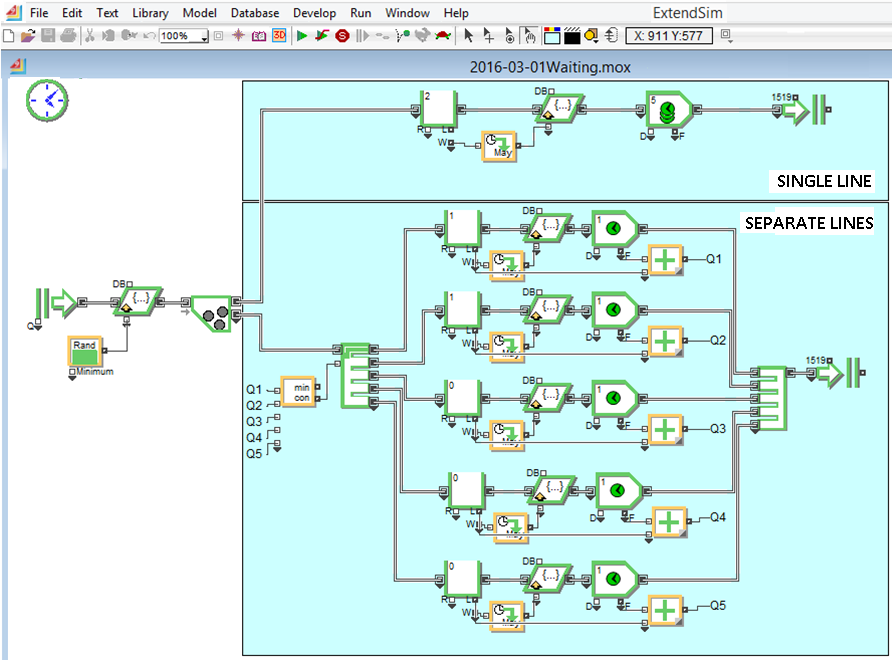
By subjecting the two systems to the same parameters, we were able to study histograms of customers waiting time.
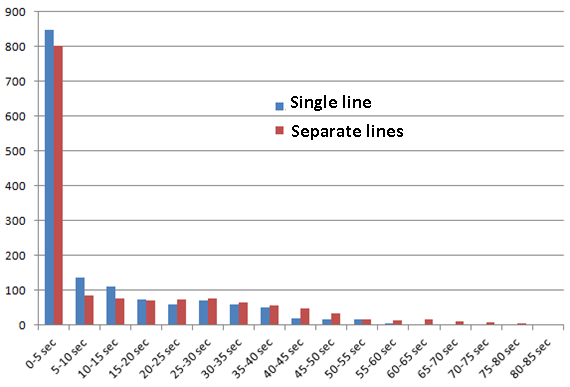
First, the blue curve shows that a single line allows for more people to be served quickly. The waiting time curve is also shorter for this system.
The mean and standard deviation for waiting times give the following results:
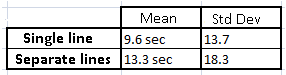
The difference between standard deviations is easy to explain. Indeed, in separate lines, a customer with a longer service time will significantly penalize the waiting time, but only for customers behind him. In a single line, the same customer would penalize every other customer even though this delay is better distributed. This is the reason why a single line is a fairer system, besides the first in, first out principle.
Which might seem more surprising is the difference in average waiting times. Why such a difference when we used the exact same characteristics for customers and counter staff? When we analyze the simulation run, especially the animation, the answer comes up: in separate lines it sometimes happens, though rarely, that a counter has no more tasks to achieve while no customers are waiting in the queue. These brief moments with “nothing to do” end up penalizing overall waiting times as the resource is not used though other lines exist (let’s keep in mind that in this model customers can’t change lines).
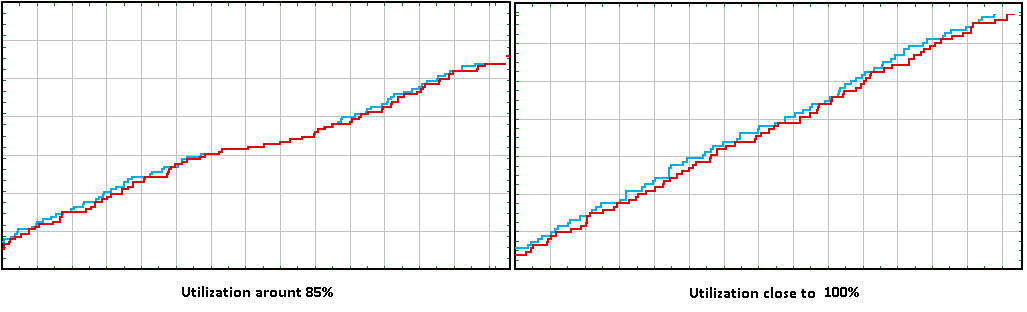
It should finally be noted that with these assumptions leading to a utilization rate of approximately 85%, the total number of people processed during these three hours is the same for both systems. Moreover, it cannot be said that the single line is more efficient in terms of resources: the difference in the number of customers served is very small and it reverses as soon as the rate of arrival slows down. However, if the systems are continuously loaded, customers from the single line (blue curve) systematically get out more quickly. This system is not only “fairer”, but also more efficient.
1) Whether you have experienced this situation or not, we invite you to watch a funny animation about this topic.